本文的原文作者为Steve Thomas(PhD),是英国威尔士Bridgend的Princess of Wales Hospital外科材料实验室的主任,原文发表于2003年EWMA杂志第3卷。虽然是一篇旧文,但其内容对于解决目前临床绷带应用中的诸多实践问题有很大帮助。
实践中很多临床人员对于如何获得最佳绷带下压力感到头痛,虽然有压力测量仪器可以测量,但不可能每个患者都使用,这也影响了压力治疗的效果和接受度。因此,如果能掌握一些压力治疗的原则和估算压力的方法,相信对临床工作大有裨益。这也是作者写此文的目的。
要点:
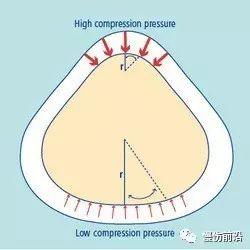
- 根据Laplace(拉普拉斯)定律,绷带下压力与绷带张力正相关,但与肢体曲率半径成反比;
- 当使用Laplace定律来估算绷带下压力时,须考虑另外两个因素,即绷带宽度和绷带层数;
- 绷带的应用方法和技巧也对初始绷带下压力有重要影响;
- 计算所得的绷带下压力是绷带对已知周长肢体所施加的平均压力。使用衬垫可以减少局部压力的变化差异。
压力治疗用于治疗水肿和其它下肢静脉和淋巴疾病已经有数个世纪,其是简单下肢静脉溃疡的标准治疗方法。Laplace定律可以用于计算或估计绷带下压力(Sub-bandage pressure),即绷带向肢体施加的压力水平。本文将解释Laplace方程的建立,以及如何用其在临床实践中估算绷带下压力。
绷带所能产生的压力水平是四种主要因素间复杂的相互作用的结果,这些因素包括:
- 绷带的物理结构和弹性
- 肢体的尺寸和形状
- 使用者的技术和手法
- 患者的活动能力
绷带所能产生的压力是绷带张力(Tension)、层数(Layers)、和肢体曲率半径(Radiusof limb curvature)的函数。这些因素之间的关系由Laplace定律确定,即绷带下压力与绷带张力成正比,但与肢体曲率半径成反比。
尽管Laplace定律被用于解释压力治疗原理已经有很久的历史[1-3],但人们对其理解仍然有限。1990年,Thomas等发表了一种改进的Laplace方程,旨在解决这一问题[4]。此后发表的文献虽然大量引用此方程,但很少解释如何在临床实践中使用此方程估算绷带下压力。
Laplace方程
用以估算绷带下压力的Laplace方程源自1805年由ThomasYong和PierreSimon de Laplace分别独立发表的公式。当年的公式是用来描述封闭的弹性膜或液体球形膜内外压力差与膜张力之间的关系[8]。
Pa – Pb = 2Y/r
公式中的Pa和Pb分别代表膜表面内外的压力,r是曲面半径,Y是膜张力。公式表明表面内的压力永远大于表面外压力,但压力差随着半径变大而减小(半径无限大时表面为平面);相反压力差随着半径变小而增大。
当计算柱状体壁压力时,公式变为P=T/r(T为张力,r为半径)。因为当半径和内部压力一定的情况下,球形容器壁的张力是柱状体的一半。
该定律在很多科学领域均有应用,包括物理化学、化学工程学、以及生命科学等。其可用来解释微小颗粒的特性、计算固体金属表面能量、计算血管压力以及充满液体的肺泡的压力等[8]。
当使用公式P=T/r时,须使用的单位为:帕斯卡(压强)、米(长度)、牛顿(力)。但这些单位并不常用于医学实践中,我们需要将其转化为人们更加熟悉的单位,例如mmHg、cm、和Kgf(kilogramforce)。此外,柱状体(肢体)的尺寸在原公式里用半径代表,但实践中无法简单的测量肢体半径。因此,我们改用周长代替。各种单位的转换因子见表1。
| Table 1: 单位转换 | |||
| 参数 | 通用单位 | 临床常用单位 | 转换因子 |
| 压力 | Pascal | mmHg | 0.0075 |
| 力 | Newton | Kgf | 0.102 |
| 长度 | Metre | Centimetre | 100 |
| Radius | Circumference | 2π r = (2 x 3.142r) | |
使用Laplace方程计算绷带下压力时,我们还必须考虑另外两个因素:绷带的宽度和层数。
绷带宽度的重要性
对于球囊或血管,壁的张力作用于整个表面。相反,对于覆盖柱状体或肢体的单层绷带来说,压力仅作用于绷带覆盖的有限区域。那么单位面积承受的压力(压强)将由绷带的总张力和绷带的宽度决定,压强=力/单位面积。这意味着使用同样的力(F),10cm宽绷带下的压力仅为5cm宽绷带下压力的一半。绷带的张力在公式中表示为“力/单位宽度”。
绷带层数
绷带拥有的总张力是其每一根纺线(yarn)的张力的总和。因此,我们可以理解当你用同样力道打两层绷带时,覆盖肢体表面的绷带纤维(纺线)数量将翻倍,局部压力也将加倍。因此,计算绷带下压力时须考虑绷带层数(n)。
用一个例子来说明如何在临床中使用Laplace方程计算绷带下压力,注意所用单位的转换:
单层绷带0.1m宽(10cm),肢体半径0.05m(周长31.416cm),绷带张力20牛顿(2.04KgF)。使用通用单位计算绷带下压力如下:

使用临床常用单位计算常数K,如下:

对于单层绷带(n=1),公式计算得出K为4620;因此,计算绷带下压力的公式可以总结为:

讨论
我们须了解使用此公式计算所得的绷带下压力仅适用于绷带刚打好时。随着时间的推移,大部分绷带的张力会显著下降,而压力也随之减小。公式中绷带的宽度亦指绷带打好的那一刻,有些绷带随着被不断的拉伸其宽度会显著减小。因此,在计算时要使用的宽度应是拉伸后的宽度,而不是未被拉伸或正常宽度。
其它决定初始绷带下压力的重要因素是绷带应用的方法。上述例子中的情形是单层绷带以与肢体垂直的方向进行缠绕。而在实践中,更常用螺旋法等技术,绷带会有不同程度的重叠,即表明在肢体表面不同部位会有不同层数的绷带覆盖。50%的重叠会形成有效的双层绷带,但66%的重叠会形成三层覆盖的情况。由于此原因,当使用高弹力绷带进行包扎时应特别小心,避免过多重叠,以免在局部形成过高的压力而导致组织损伤甚至坏死。
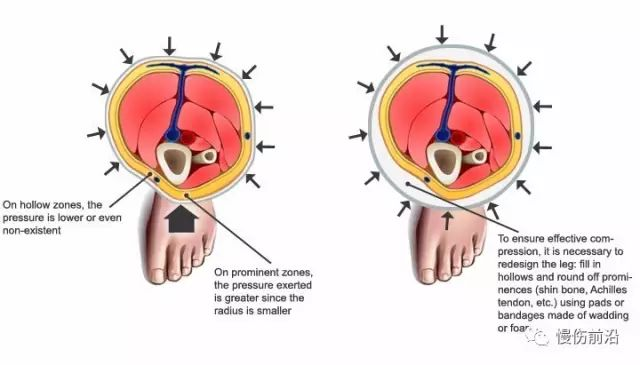
计算所得的绷带下压力是绷带在已知周长肢体上产生的平均压力。如果将绷带打在截面均匀一致的柱状体时,绷带下产生的压力在整个表面都是一样的。然而,人体的肢体在不同部位的曲率半径有很大差异,即便在同一截面的不同点也可能有极大差异,如果使用压力测量计进行直接测量的话,我们会发现不同部位的压力值差异非常大,与计算所得的压力值也会大不同。因此,实践中我们建议在骨突(足踝)、明显凹凸(足跟)解剖部位使用衬垫来平滑曲面,将局部压力的差异降低至可接受范围。

结论
由于实践中测量绷带下压力有很多实际困难,因此人们希望用Laplace方程来估算在特定张力下绷带产生的压力。然而,对于Laplace定律的应用,迄今为止人们的理解仍然不深,包括对于绷带宽度和层数认识。本文希望能帮大家解决这些疑问,更好地在临床中应用相关知识,改善治疗技术和效果。
内容转载自@慢伤前沿公众号!
